Vous êtes en train de jongler avec les trinômes du second degré et vous vous demandez comment arriver à leur forme factorisée ? Ne cherchez pas plus loin ! La factorisation d’un trinôme peut sembler difficile, mais il existe des méthodes simples pour y parvenir, comme la règle du discriminant. Que ce soit pour des fonctions polynomiales ou des équations, il est crucial de comprendre non seulement la théorie, mais aussi les applications pratiques.
Si vous avez des questions ou si vous souhaitez approfondir vos connaissances en mathématiques, notre équipe est là pour vous aider. N’attendez plus, contactez-nous dès maintenant ! Chaque question mérite une réponse et chaque trinôme mérite d’être compris.
Rendez-vous sur notre page de contact pour échanger avec nos experts et résoudre toutes vos préoccupations :
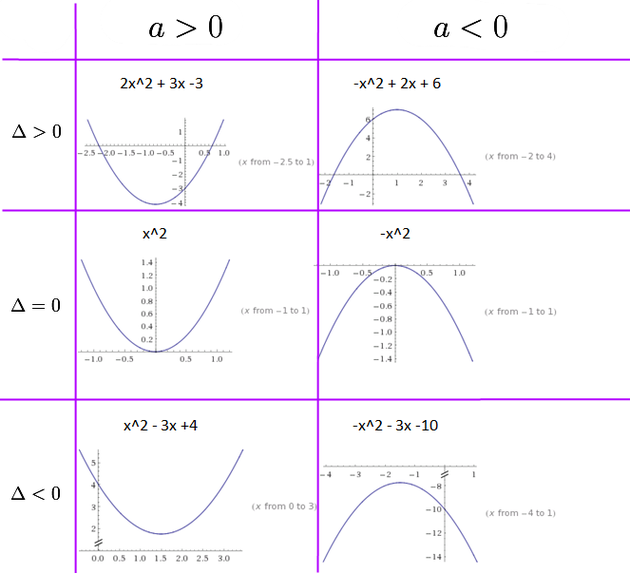
Pour trouver la forme factorisée d’un trinôme, il est essentiel de partir de l’expression sous la forme générale ax² + bx + c. La première étape consiste à calculer le discriminant (Δ) selon la formule Δ = b² – 4ac. Ce calcul permet de déterminer la possibilité de factorisation. Si Δ est supérieur à zéro, le trinôme se factorise sous la forme a(x – x₁)(x – x₂), où x₁ et x₂ sont les racines trouvées grâce à la formule quadratique. Si Δ est égal à zéro, la factorisation prend la forme a(x – r)², avec r étant la racine double. En revanche, si Δ est inférieur à zéro, le trinôme ne peut pas se factoriser dans le domaine des nombres réels. Par conséquent, le discriminant joue un rôle crucial dans le processus de factorisation d’un trinôme du second degré.
La factorisation d’un trinôme de la forme ax² + bx + c est une compétence cruciale en mathématiques. Ce processus permet de simplifier les équations et de résoudre divers problèmes mathématiques. Cet article explore les avantages et inconvénients de la factorisation des trinômes, en se concentrant sur les méthodes et résultats associés.
Avantages
L’un des principaux avantages de trouver la forme factorisée d’un trinôme est la simplification des calculs. En effet, une fois factorisé, il est souvent plus facile d’identifier les racines de l’équation. Cela est particulièrement vrai lorsque le discriminant est supérieur ou égal à zéro, ce qui indique la possibilité de factoriser pour obtenir les racines directement.
De plus, maîtriser la factorisation permet de comprendre des concepts plus avancés, comme la résolution d’équations quadratiques ou l’analyse de paraboles. Grâce à la forme factorisée, vous pouvez rapidement déterminer les points d’intersection avec l’axe des abscisses, ce qui est essentiel dans de nombreux domaines, comme la physique ou l’économie.
Inconvénients
Contactez-nous dès maintenant !
Vous avez des questions ou besoin d’une assistance concernant nos services de transport et de déménagement ? Ne laissez pas vos doutes s’accumuler ! Notre équipe d’experts est prête à vous apporter toutes les précisions nécessaires.
Découvrez comment nous pouvons vous aider à réaliser vos projets en toute sérénité. Chaque déménagement est unique, et nous sommes là pour vous guider avec des solutions adaptées à vos besoins.
Ne tardez plus, contactez-nous dès aujourd’hui et obtenez des réponses rapides et précises.

Comparaison des méthodes de factorisation d’un trinôme
| Critère/Étape | Description concise |
| Forme générale | Représenter le trinôme sous la forme ax² + bx + c |
| Calcul du discriminant (Δ) | Δ = b² – 4ac, clé pour déterminer les racines |
| Existence de racines | Δ > 0 : deux racines réelles, Δ = 0 : une racine double |
| Factorisation directe | Pour Δ > 0, f(x) = a(x – x1)(x – x2) |
| Forme canonique | f(x) = a(x – α)² + β, pour simplifier l’intégration |
| Simplification | Regrouper pour faciliter l’analyse et la visualisation |
| Vérification | Développer la forme factorisée pour confirmer l’exactitude |

Comment trouver la forme factorisée d’un Trinôme ?
La factorisation d’un trinôme est une étape clé en mathématiques, permettant de simplifier les calculs et de résoudre des équations. Cet article vous montrera comment déterminer la forme factorisée d’un trinôme du second degré, avec une attention particulière sur la méthode des racines et le calcul du discriminant. Vous apprendrez à identifier les conditions sous lesquelles un trinôme peut être factorisé, ainsi que les étapes à suivre pour y parvenir.
Comprendre la forme d’un trinôme
Un trinôme se présente généralement sous la forme ax² + bx + c, où a, b et c sont des coefficients. Pour factoriser ce trinôme, il est essentiel de comprendre comment il interagit avec ses racines. Si le trinôme est écrit sous la forme factorisée a (x – u)(x – v), alors les racines du trinôme sont u et v. La connaissance de ces racines est primordiale pour effectuer la factorisation.
Calculer le discriminant
Le discriminant d’un trinôme est un élément fondamental pour déterminer sa factorisation. Il est calculé à l’aide de la formule Δ = b² – 4ac. En fonction de la valeur du discriminant, on peut établir trois cas différents :
- Si Δ > 0, le trinôme a deux racines distinctes et peut être factorisé sous la forme a(x – x₁)(x – x₂).
- Si Δ = 0, le trinôme a une racine double, ce qui signifie qu’il peut être écrit sous la forme a(x – x₁)².
- Si Δ
La méthode de la factorisation par la formule quadratique
La méthode des racines est une approche essentielle pour factoriser un trinôme. Lorsque le discriminant est calculé comme décrit précédemment, il permet de déterminer les racines réalisables (x₁ et x₂). Par la suite, vous pouvez expressément reformuler le trinôme à l’aide de ces racines, vous assurant ainsi que les résultats soient corrects. Cette technique est un outil puissant pour aider à résoudre des équations quadratiques.
Forme canonique
Une autre manière utile d’aborder la factorisation consiste à trouver la forme canonique d’un trinôme. La forme canonique s’exprime comme f(x) = a(x – α)² + β, où α et β représentent les valeurs spécifiques dérivées du trinôme initial. Cette méthode est particulièrement bénéfique pour visualiser la courbe associée et voir comment le trinôme se comporte dans un plan graphique.
Pour obtenir une factorisation réussie d’un trinôme du second degré, il est crucial de bien comprendre son maniement et d’utiliser les outils mathématiques adéquats tels que le discriminant et la méthode des racines. Grâce à ces connaissances, tout élève peut acquérir les compétences nécessaires pour maîtriser la factorisation des trinômes. Pour approfondir vos compétences, n’hésitez pas à consulter des ressources supplémentaires sur la factorisation des trinômes et la calcul du coût de transport.
Introduction à la Factorisation des Trinômes
La factorisation d’un trinôme est une étape essentielle en mathématiques, notamment pour résoudre des équations quadratiques. Comprendre comment trouver la forme factorisée d’un trinôme vous permet de simplifier des expressions et de mieux appréhender les concepts polynomiaux.
Identification de la Forme du Trinôme
Un trinôme se présente généralement sous la forme ax² + bx + c, où a, b, et c sont des coefficients. La première étape consiste à s’assurer que le coefficient a n’est pas égal à 1, car cela change légèrement la méthode de factorisation à utiliser.
Calcul du Discriminant
Pour déterminer si un trinôme peut être factorisé, il est indispensable de calculer le discriminant, symbolisé par Δ. La formule est donnée par Δ = b² – 4ac. Trois cas peuvent se présenter :
- Δ > 0 : Il existe deux racines réelles distinctes, permettant une factorisation dans la forme a(x – x1)(x – x2).
- Δ = 0 : Il y a une racine double, et le trinôme se factorise en a(x – r)², où r est la racine.
- Δ Dans ce cas, le trinôme n’est pas factorisable dans le domaine des nombres réels.
Utilisation de la Formule Quadratique
Si le discriminant est positif ou nul, la formule quadratique est une méthode puissante pour trouver les racines. Les racines peuvent être calculées via x = (-b ± √Δ) / (2a). Ces valeurs de x peuvent ensuite être placées dans la forme factorisée.
Transformation de Trinômes sous Forme Factorisée
Une fois que les racines sont connues, le trinôme peut être réécrit sous forme factorisée. Pour le cas où les racines sont x1 et x2, la forme factorisée prendra la forme a(x – x1)(x – x2). Cette étape maximise la clarté et facilite le calcul ultérieur.
Exemples de Factorisation
Pour illustrer ce processus, considérons un exemple pratique :
Supposons que nous avons le trinôme 2x² – 4x – 6. D’abord, nous calculons le discriminant :
Δ = (-4)² – 4 × 2 × (-6) = 16 + 48 = 64.
Étant donné que Δ > 0, nous appliquons la formule quadratique pour trouver les racines et ensuite déterminer la forme factorisée.
La factorisation d’un trinôme du second degré ne se limite pas à une simple technique; elle exige une compréhension approfondie des concepts mathématiques sous-jacents comme le calcul du discriminant et l’application de la formule quadratique. En maîtrisant ces méthodes, il devient plus facile de travailler avec des polynômes et de résoudre des équations mathématiques complexes.
La factorisation d’un trinôme du second degré est une étape clé en mathématiques, particulièrement dans le cadre de la résolution d’équations quadratiques. Cette opération consiste à écrire un trinôme sous une forme qui révèle ses racines. Cet article vous guide à travers les différentes méthodes pour obtenir la forme factorisée d’un trinôme, en abordant les notions de discriminant et de techniques de mise en œuvre.
Comprendre le trinôme du second degré
Un trinôme du second degré peut être exprimé sous la forme générale ax² + bx + c, où a, b et c sont des coefficients réels et a ≠ 0. Lorsqu’on cherche à factoriser un trinôme, on tente de le réécrire sous la forme a(x – u)(x – v), où u et v sont les racines du trinôme. Cela permet de simplifier les calculs lors de la résolution d’équations composite.
Règle du discriminant
Pour déterminer si un trinôme peut être factorisé, il est essentiel de calculer le discriminant Δ, donné par la formule Δ = b² – 4ac. Trois cas se présentent :
- Δ : Le trinôme n’a pas de racines réelles et ne peut pas être factorisé.
- Δ = 0 : Il existe une racine double, ce qui signifie que le trinôme peut être factorisé de manière unique.
- Δ > 0 : Deux racines distinctes existent, et le trinôme peut être factorisé en utilisant ces racines.
Méthodes de factorisation
Une fois le discriminant calculé, plusieurs méthodes peuvent être appliquées pour trouver la forme factorisée d’un trinôme :
- Utilisation de la formule quadratique : Cette méthode s’applique lorsque Δ ≥ 0 et permet de trouver les racines u et v à l’aide de la formule u, v = (-b ± √Δ) / (2a).
- Méthode de la recherche des facteurs : Si le trinôme est de la forme ax² + bx + c, chercher deux nombres dont le produit est ac et dont la somme est b peut aider à établir les facteurs.
- Complétion du carré : Cette méthode consiste à réécrire le trinôme sous sa forme canonique, facilitant ainsi l’identification de ses racines.
Application de la factorisation
Une fois la forme factorisée trouvée, il est possible d’utiliser les racines pour résoudre des équations. En effet, s’il est établi que f(x) = a(x – u)(x – v), l’équation f(x) = 0 indique directement que les solutions sont x = u et x = v.
Ressources complémentaires
Pour approfondir vos connaissances sur la factorisation des trinômes, vous pouvez consulter des ressources utiles telles que Alloprof ou Khan Academy.
La factorisation d’un trinôme du second degré est une étape essentielle dans l’étude des polynômes. Que vous soyez élève, étudiant ou simplement curieux, comprendre comment aboutir à la forme factorisée d’un trinôme vous permettra d’approfondir vos connaissances en mathématiques. Imaginez pouvoir résoudre facilement des équations et analyser des fonctions !
Il existe des méthodes passionnantes, telles que la formule quadratique, qui vous aideront à identifier les racines du trinôme. En maîtrisant ces techniques, vous gagnerez en confiance et en compétence. Mais pourquoi s’arrêter là ? Les applications de ces concepts ne se limitent pas aux maths, elles trouvent également des résonances dans des domaines variés, comme la logistique et le transport.
Si vous souhaitez aller plus loin et explorer plus en profondeur ces notions, n’hésitez pas à nous contacter pour toute question ou besoin d’assistance. Votre curiosité est le meilleur moteur pour apprendre et progresser !
Ne restez pas dans l’ombre, faites le premier pas ! Visitez notre page de contact et discutons de vos besoins. Nous serons ravis de vous aider dans votre apprentissage !

La factorisation d’un trinôme est une procédure mathématique cruciale qui permet d’exprimer une équation de degré deux sous une forme plus simplifiée. Cette étude se concentre sur comment déterminer la forme factorisée d’un trinôme du second degré, ce qui implique l’usage de la formule quadratique ainsi que le calcul du discriminant. En suivant cette méthode, il est possible de trouver les racines du polynôme et de rédiger son expression factorisée.
Identification de la forme du trinôme
Un trinôme du second degré se présente généralement sous la forme ax² + bx + c, où a, b et c sont des coefficients réels et a ≠ 0. La première étape consiste à identifier ces coefficients afin de pouvoir appliquer les techniques appropriées. Il est essentiel de s’assurer que le trinôme est bien en forme standard avant de continuer.
Calcul du discriminant
Le discriminant est une partie fondamentale dans la factorisation d’un trinôme. Il se calcule avec la formule suivante : Δ = b² – 4ac. Ce calcul permettra de déterminer le nombre de solutions réelles que possède le trinôme. En effet, si Δ > 0, alors il existe deux racines distinctes. Si Δ = 0, il y a une unique racine. En revanche, si Δ , le trinôme ne se factorise pas dans le domaine des réels.
Application de la formule quadratique
Pour les cas où Δ ≥ 0, il est possible d’utiliser la formule quadratique : x = (-b ± √Δ) / (2a). Cette formule permet de calculer les racines du trinôme, que l’on notera x1 et x2. Exprimées ainsi, les racines offrent un moyen de construire la forme factorisée du trinôme sous la forme : a(x – x1)(x – x2).
Fautes à éviter
Il est crucial de prêter attention à certains points lors de la factorisation. Assurez-vous de ne pas négliger le coefficient a. Si ce coefficient est différent de 1, chaque terme de la forme factorisée doit être multiplié par a pour garantir la précision de l’équation. Il est également conseillé de vérifier chaque étape de votre calcul pour éviter des erreurs d’addition ou de soustraction qui pourraient déformer les résultats.
Exemples pratiques
Pour illustrer ce processus, prenons un trinôme tel que 2x² + 5x + 3. En identifiant les coefficients, nous trouvons a = 2, b = 5, et c = 3. Calculons le discriminant : Δ = 5² – 4(2)(3) = 25 – 24 = 1, ce qui indique deux racines distinctes. En utilisant la formule quadratique, nous obtenons x1 = -1 et x2 = -3/2. Finalement, la forme factorisée est 2(x + 1)(x + 3/2).
Pour approfondir vos connaissances sur la factorisation des trinômes, visitez les ressources : WikiHow sur la factorisation et Labomath pour des leçons détaillées.
La factorisation d’un trinôme est une étape essentielle dans le traitement des polynômes du second degré. Pour un trinôme de la forme ax² + bx + c, il s’agit de le réécrire sous la forme d’un produit de deux binômes. Cette procédure est particulièrement utile dans de nombreux domaines mathématiques, notamment pour la résolution d’équations et l’étude des racines. Dans cet article, nous allons explorer les étapes et les méthodes à suivre pour parvenir à cette forme factorisée.
Compréhension du Trinôme
Avant d’entamer la factorisation, il est crucial de bien comprendre la structure du trinôme. La forme générale est a x² + b x + c, où a, b et c sont des coefficients numériques. Lors de la factorisation, on cherche à exprimer le trinôme comme un produit de deux binômes, ce qui est souvent possible si le discriminant Δ = b² – 4ac est supérieur ou égal à zéro. Cela conditionne la capacité de factoriser le trinôme et d’en extraire les racines.
Utilisation de la Formule Quadratique
Une méthode efficace pour factoriser un trinôme consiste à utiliser la formule quadratique. Cette méthode est particulièrement recommandée si le coefficient a est différent de 1. En calculant le discriminant, on peut déterminer les racines du trinôme, à savoir x₁ et x₂, via la formule : x = (-b ± √Δ) / (2a). Une fois les racines trouvées, la factorisation s’effectue facilement sous la forme a(x – x₁)(x – x₂).
Cas Particuliers de Factorisation
Il est important de noter différents scénarios rencontrés lors de la factorisation d’un trinôme. Si le discriminant est négatif (Δ
Autres Techniques de Factorisation
Outre la méthode de la formule quadratique, il existe d’autres techniques de factorisation, telles que la complétion du carré. Cette méthode consiste à réécrire le trinôme en ajoutant et soustrayant une valeur nécessaire pour obtenir un carré parfait. Cela mène directement à la forme canonique, à partir de laquelle on peut dériver la forme factorisée. Ces approches offrent plus de flexibilité pour la manipulation des trinômes complexes.
Pratique et Applications
Enfin, la pratique est essentielle pour maîtriser la factorisation des trinômes. De nombreux exercices disponibles en ligne permettent de renforcer cette compétence, comme ceux proposés par Maths et Tiques ou Afterclasse. Comprendre chaque étape du processus garantira une meilleure maîtrise des mathématiques et des applications dans des domaines variés tels que la physique ou l’ingénierie.
Comment trouver la forme factorisée d’un Trinôme ?
Pour trouver la forme factorisée d’un trinôme, il est essentiel de commencer par analyser la structure du trinôme qui prend généralement la forme ax² + bx + c, où a, b et c sont des coefficients. La première étape consiste à calculer le discriminant (Δ) du trinôme, donné par la formule Δ = b² – 4ac. Ce discriminant jouera un rôle clé dans la détermination de la factorisation.
En effet, selon la valeur de Δ, on peut conclure sur la possibilité de factoriser le trinôme. Si Δ est supérieur à zéro, cela signifie qu’il existe deux racines distinctes pour ce trinôme, ce qui permet de le factoriser sous la forme f(x) = a(x – x₁)(x – x₂), où x₁ et x₂ sont les racines obtenues en utilisant la formule des racines : x = (-b ± √Δ) / (2a).
Dans le cas où Δ est égal à zéro, on a une racine double, et la forme factorisée pourrait s’exprimer comme f(x) = a(x – u)², où u est la valeur de la racine. En revanche, si Δ est inférieur à zéro, cela indique que le trinôme n’a pas de racines réelles, et donc il ne peut pas être factorisé au sens traditionnel du terme.
Dernièrement, pour faciliter le processus de factorisation, il peut s’avérer utile d’étudier la forme canonique d’un trinôme, qui est f(x) = a(x – α)² + β. Cette méthode permet de visualiser la situation des racines de manière graphique, enrichissant ainsi la compréhension globale du trinôme. La factorisation d’un trinôme s’avère ainsi être une démarche logique qui peut être aisément suivie avec un minimum de pratique.
FAQ – Comment trouver la forme factorisée d’un Trinôme ?
Un trinôme du second degré est une expression polynomiale de la forme ax² + bx + c, où a, b et c sont des coefficients réels et a est différent de zéro.
Le discriminant d’un trinôme est calculé avec la formule Δ = b² – 4ac. Il permet de déterminer le nombre de racines réelles du trinôme.
Un discriminant positif indique que le trinôme a deux racines réelles distinctes, ce qui permet de le factoriser sous la forme f(x) = a(x – x1)(x – x2).
Lorsque le discriminant est égal à zéro, cela signifie que le trinôme a une seule racine réelle, et il peut être factorisé sous la forme f(x) = a(x – u)².
Un discriminant négatif indique que le trinôme n’a pas de racines réelles et ne peut donc pas être factorisé dans le domaine des réels.
La forme canonique d’un trinôme peut être trouvée en utilisant la méthode de la complétion du carré, ce qui donne l’expression f(x) = a(x – α)² + β.
Témoignages sur la factorisation d’un trinôme et mestransporteurs.fr
La factorisation d’un trinôme s’avère souvent être un défi pour de nombreux étudiants. Pour moi, la méthode a véritablement changé ma perception des mathématiques. En comprenant que chaque trinôme peut être exprimé sous la forme de produits de binômes, j’ai réalisé que la formule quadratique était ma meilleure amie. Elle permet de résoudre de manière efficace et rapide; dès que j’ai commencé à l’utiliser, mes résultats se sont améliorés et ma confiance en moi a fait un bond. Le processus devient presque intuitif lorsque l’on s’entraîne régulièrement.
En tant qu’expert, je fais souvent le parallèle entre la factorisation d’un trinôme et la planification d’un transport efficace. Il s’agit de décomposer un problème complexe en éléments plus simples afin de le résoudre. La première étape consiste à calculer le discriminant, qui permet de déterminer la nature des racines du trinôme. Savoir si ce dernier peut se factoriser ou non est essentiel, tout comme comprendre les coûts de transport pour optimiser un projet logistique.
Lorsque j’ai découvert mestransporteurs.fr, j’ai été impressionné par leur approche orientée client dans le domaine du déménagement. Ils ont su rendre le processus transparent et accessible, un peu comme une bonne méthode de factorisation. Le site offre un calculateur qui permet d’estimer facilement les coûts en fonction de divers paramètres tels que la distance, la taille de la cargaison, ou encore le type de transports. Cela permet de maîtriser le budget, tout comme visualiser les coefficients dans un trinôme pour mieux appréhender sa structure.
Leur plateforme offre également des conseils pratiques, un peu comme les étapes que l’on suit en factorisant un trinôme. Chaque étape est cruciale, et avoir un guide fiable pour tous vos besoins en transport est similaire à avoir une méthode claire pour parvenir à la forme factorisée d’un polynôme. En fin de compte, que ce soit pour les maths ou la logistique, une bonne organisation et des outils adéquats peuvent faire toute la différence dans la réussite.
Vous êtes en plein apprentissage de la factorisation des trinômes du second degré et vous vous demandez comment maîtriser cette compétence essentielle ? Ne restez pas dans le flou, il est temps d’accéder à des conseils pratiques et des ressources adaptées pour vous aider à réussir cette étape importante.
Notre équipe est prête à vous guider dans votre compréhension et maîtrise des formules quadratiques et des discriminants. Que vous soyez élève, étudiant ou simplement passionné par les mathématiques, nos experts sont là pour répondre à toutes vos questions.
N’attendez plus pour enrichir vos connaissances ! Contactez-nous dès aujourd’hui pour obtenir l’aide et les informations dont vous avez besoin. Cliquez sur le lien suivant et faites le premier pas vers la réussite : Visitez notre page de contact.
Comment trouver la forme factorisée d’un Trinôme ?
La factorisation d’un trinôme du second degré est une étape cruciale en mathématiques, surtout dans le cadre de la résolution d’équations polynomiales. Un trinôme est généralement exprimé sous la forme ax² + bx + c, où a, b et c sont des coefficients réels et a ≠ 0. La clé pour factoriser un trinôme réside dans le calcul du discriminant Δ, qui est défini par la formule Δ = b² – 4ac.
Il existe trois situations différentes basées sur la valeur du discriminant. Si Δ est strictement négatif (Δ
Dans le cas où Δ est égal à zéro (Δ = 0), le trinôme possède une racine réelle double. Cela signifie qu’il peut être factorisé sous la forme a(x – r)², où r est la racine unique du trinôme. Pour trouver cette racine, il suffit d’utiliser la formule r = -b/(2a).
Enfin, si Δ est strictement positif (Δ > 0), le trinôme a deux racines réelles distinctes qui peuvent être calculées à l’aide de la formule quadratique. Les racines x₁ et x₂ peuvent être déterminées comme suit : x₁ = (-b + √Δ) / (2a) et x₂ = (-b – √Δ) / (2a). Ces deux racines permettent alors de factoriser le trinôme sous la forme a(x – x₁)(x – x₂).
Pour résumer, la méthode pour trouver la forme factorisée d’un trinôme implique des étapes claires : calculer le discriminant, déterminer le nombre de racines réelles, puis les utiliser pour factoriser le trinôme si cela est possible. Ce processus simple et méthodique facilite grandement la compréhension de la structure d’un polynôme du second degré.
Une autre méthode qui peut être appliquée est la complétion du carré, qui permet aussi d’obtenir la forme canonique d’un trinôme. En réécrivant le trinôme ax² + bx + c dans une forme qui met en évidence ses racines, on découvre qu’il est possible d’exprimer le trinôme comme a(x – α)² + β, où α et β sont calculés à partir des coefficients du trinôme initial.
Maîtriser la technique de la factorisation est non seulement essentiel pour réussir en mathématiques académiques, mais cela est également très utile dans des domaines pratiques comme l’économie, l’ingénierie ou même la recherche opérationnelle. En effet, savoir réduire les polynômes peut simplifier de nombreuses analyses et résoudre efficacement des problèmes complexes.
En conclusion, la factorisation d’un trinôme est une compétence fondamentale qui nécessite une bonne compréhension du comportement des polynômes en fonction de leurs racines et de leur discriminant. Une pratique régulière et une mise en application de ces principes aideront à devenir plus habile dans ce domaine mathématique fascinant.