Si vous êtes en quête de compréhension des trinômes du second degré et de leurs racines, vous êtes au bon endroit ! Nos experts en mathématiques sont là pour vous guider à travers chaque étape de ce processus fondamental. Connaître les racines d’un trinôme, c’est essentiel non seulement en mathématiques, mais également dans divers domaines d’application.
Ne laissez pas des concepts mathématiques complexes vous freiner ! Apprenez à déterminer le discriminant et à résoudre les équations pour trouver ces précieuses racines. Pour aller plus loin et explorer des ressources adaptées à votre niveau, nous vous invitons à rejoindre notre communauté.
Pour toute question ou besoin d’aide, n’hésitez pas à nous contacter. Visitez notre page de contact pour obtenir des réponses personnalisées et commencer votre parcours d’apprentissage dès aujourd’hui : Contactez-nous maintenant !
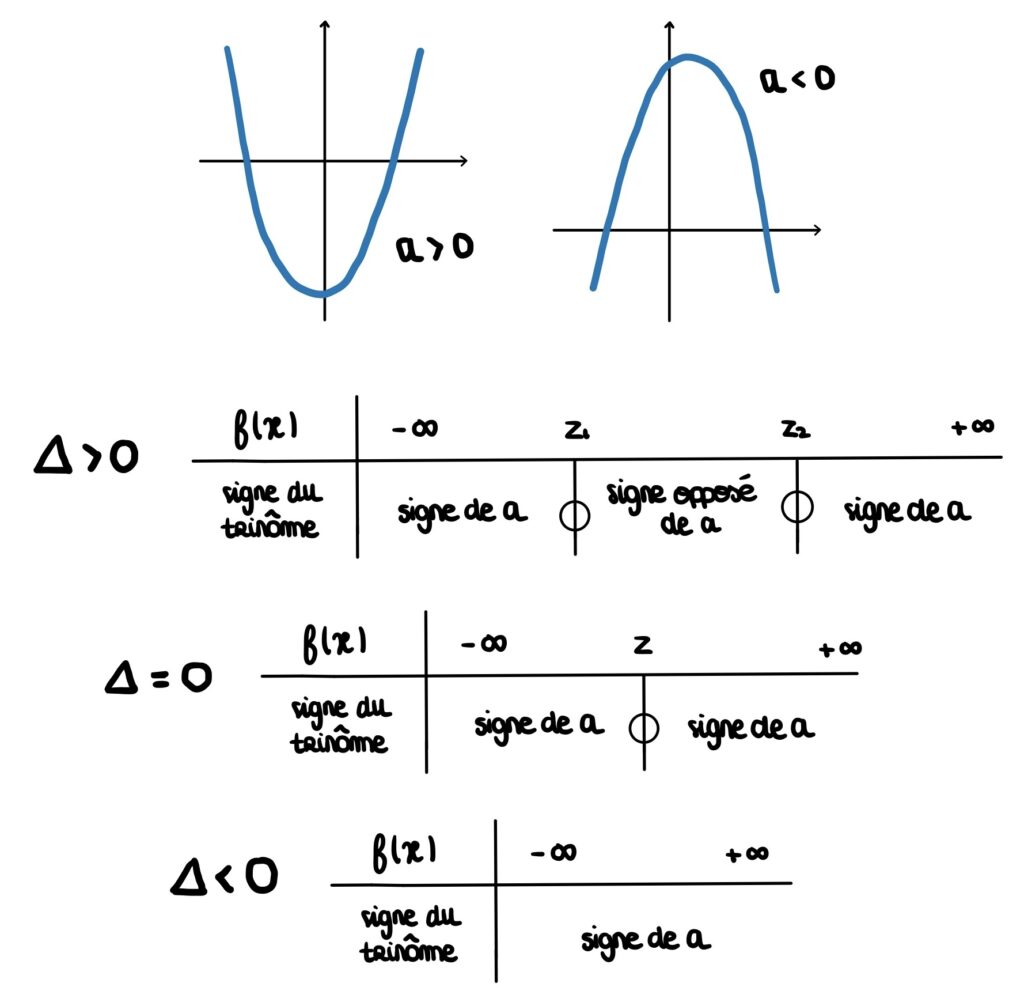
Pour calculer les racines d’un trinôme du second degré, il est essentiel de considérer l’équation de la forme ax² + bx + c = 0. La première étape consiste à déterminer le discriminant, noté Δ, qui se calcule avec la formule Δ = b² – 4ac. Le signe du discriminant informe sur le nombre de racines réelles :
- Si Δ > 0, l’équation possède deux racines réelles distinctes.
- Si Δ = 0, il existe une racine double.
- Si Δ , l’équation n’a aucune racine réelle.
Les racines réelles, lorsqu’elles existent, peuvent être trouvées en utilisant les formules :
- x₁ = (-b – √Δ) / (2a)
- x₂ = (-b + √Δ) / (2a)
Cette méthode est fondamentale pour une bonne compréhension des polynômes du second degré et leur résolution.
Comment calculer les racines d’un Trinôme ?
Le calcul des racines d’un trinôme du second degré est une compétence essentielle en mathématiques. Cela permet de comprendre comment résoudre une équation sous la forme générale ( P(x) = ax^2 + bx + c = 0 ). Utiliser le discriminant, une notion clé dans ce processus, facilite le travail en déterminant la nature des racines et leur nombre.
Avantage
Un des principaux avantages du calcul des racines d’un trinôme est sa méthode systématique et bien définie. En utilisant la formule du discriminant ( Delta = b^2 – 4ac ), nous pouvons facilement déterminer le nombre de racines réelles de l’équation.
Si le discriminant est positif, l’équation a deux racines distinctes. Si, en revanche, il est nul, cela indique la présence d’une racine double. Enfin, un discriminant négatif signifie qu’il n’y a pas de solution réelle. Ces informations permettent de mieux comprendre la représentation graphique du trinôme et ses intersections avec l’axe des abscisses, un concept fondamental pour les étudiants en mathématiques.
Inconvénients
Malgré ces avantages, il existe également des inconvénients associés au calcul des racines d’un trinôme. La compréhension du discriminant et de ses implications peut poser des difficultés pour certains étudiants. En effet, la manipulation des formules peut s’avérer complexe, surtout lorsqu’il s’agit de calculs impliquant des nombres à décimales ou des fractions.
De plus, il est crucial de se rappeler que cette méthode doit être appliquée uniquement aux équations du second degré. Les étudiants peuvent parfois être tentés d’utiliser ces mêmes techniques pour des équations de degré supérieur, ce qui pourrait conduire à des erreurs. Pour approfondir les techniques de calcul des racines, il est recommandé de consulter des ressources comme Kartable ou encore des exercices pratiques sur des plateformes éducatives.
Vous avez des questions concernant nos services de transport et de déménagement ? Notre équipe est là pour vous accompagner ! Que vous ayez besoin de conseils, d’un devis personnalisé ou de plus d’informations, n’attendez plus !
Cliquez ici pour accéder à notre page de contact et obtenez une assistance rapide et professionnelle. Chaque question mérite une réponse, et nous sommes prêts à vous écouter et à vous aider.
Faites le premier pas vers un transport en toute sérénité, Contactez-nous maintenant !
Calcul des racines d’un trinôme
| Méthode | Explication |
| Calculer le discriminant | La formule est Δ = b² – 4ac. |
| Analyser le signe du discriminant | Si Δ > 0, deux racines réelles distinctes. |
| Une racine double | Si Δ = 0, une racine double. |
| Aucune racine réelle | Si Δ |
| Calcul des racines | x₁ = (-b – √Δ) / (2a) et x₂ = (-b + √Δ) / (2a). |
| Facteur commun | Si a ≠ 0, factoriser le trinôme. |

Comment calculer les racines d’un Trinôme ?
Le calcul des racines d’un trinôme du second degré est essentiel en mathématiques, notamment pour résoudre diverses équations. Il repose principalement sur l’utilisation du discriminant, qui permet de déterminer la nature et le nombre de racines réelles d’un trinôme donné. Dans cet article, nous allons explorer la méthode permettant de calculer ces racines et les différentes situations qui peuvent se présenter.
Comprendre le Trinôme du Second Degré
Un trinôme du second degré est une expression polynomiale de la forme P(x) = ax² + bx + c, où a, b et c sont des coefficients réels, et a ≠ 0. Pour déterminer où ce trinôme s’annule, c’est-à-dire pour trouver les racines, on cherche les valeurs de x telles que P(x) = 0.
Le Rôle du Discriminant
Le premier outil à utiliser dans cette démarche est le discriminant, noté Δ. Il est calculé à partir des coefficients du trinôme selon la formule suivante : Δ = b² – 4ac. Le signe de Δ nous indique le nombre et la nature des racines de l’équation :
- Δ > 0 : Il existe deux racines réelles distinctes.
- Δ = 0 : Il existe une racine double.
- Δ Il n’y a pas de racines réelles.
Calculer les Racines
Une fois le discriminant calculé, il est possible de déterminer les racines. Si Δ ≥ 0, les racines peuvent être trouvées avec les formules :
- x₁ = (-b – √Δ) / (2a)
- x₂ = (-b + √Δ) / (2a)
Ceci montre que les racines sont fonction des coefficients et de la valeur du discriminant. Dans le cas d’une racine double, les deux racines seront identiques, conduisant à une solution unique.
Application Pratique
Pour visualiser ce processus, prenons un exemple concret : considérons l’équation 3x² – 6x – 2 = 0. En appliquant notre formule pour le discriminant, nous trouvons Δ = (-6)² – 4 * 3 * (-2) = 36 + 24 = 60, qui est positif. Ainsi, nous calculons :
- x₁ = (6 – √60)/6
- x₂ = (6 + √60)/6
Ce qui nous permet de déterminer les valeurs précises de x₁ et x₂.
Le processus de calcul des racines d’un trinôme du second degré est donc largement fondé sur la compréhension de son discriminant. Pour approfondir vos connaissances et vous exercer, vous pouvez consulter des exemples pratiques sur des sites spécialisés, comme ici ou là.
Définition du trinôme du second degré
Un trinôme du second degré s’exprime généralement sous la forme ax² + bx + c, où a, b et c sont des coefficients réels et a ne doit pas être égal à zéro. Ces trinômes représentent des fonctions quadratiques dont l’étude est essentielle en mathématiques.
Le discriminant
Le discriminant, noté Δ, est un élément clé pour déterminer le nombre et la nature des racines d’un trinôme. Il se calcule à l’aide de la formule suivante : Δ = b² – 4ac. Selon la valeur du discriminant, il est possible de savoir si les racines sont réelles ou complexes.
Cas du discriminant positif
Si Δ > 0, le trinôme possède deux racines réelles distinctes. Dans ce cas, les racines peuvent être calculées à l’aide des formules suivantes :
- x1 = (-b – √Δ) / (2a)
- x2 = (-b + √Δ) / (2a)
Cas du discriminant nul
Dans le cas où Δ = 0, il existe une racine double. Cela signifie que le trinôme a une seule solution réelle, qui peut être calculée via la formule :
x = -b / (2a)
Cas du discriminant négatif
Lorsque Δ , le trinôme n’a pas de racines réelles. Dans ce scénario, les solutions sont des nombres complexes, ce qui est important à considérer dans le cadre d’études avancées en mathématiques.
Factorisation du trinôme
En fonction du discriminant, un trinôme peut être factorisé. Si Δ est supérieur ou égal à zéro, il peut être exprimé sous la forme :
a(x – x1)(x – x2), où x1 et x2 sont les racines trouvées précédemment. Pour une racine double, la factorisation prend la forme :
a(x – x1)².
Conclusion sur le calcul des racines
Comprendre comment calculer les racines d’un trinôme est essentiel pour résoudre des équations et analyser des fonctions quadratiques. En maîtrisant l’utilisation du discriminant, il est possible de déterminer facilement la nature des solutions d’un trinôme donné.
Comment calculer les racines d’un Trinôme ?
Le calcul des racines d’un trinôme du second degré est une compétence clé en mathématiques, particulièrement lorsqu’il s’agit de résoudre des équations quadratiques. Pour déterminer ces racines, on utilise le discriminant, qui est un outil essentiel. Cet article se penche sur les étapes nécessaires pour parvenir à calculer ces racines et comprendre leur signification.
Définition d’un trinôme du second degré
Un trinôme du second degré s’exprime sous la forme générale : P(x) = ax² + bx + c, où a, b, et c sont des coefficients réels et a est non nul. Les racines de cette équation correspondent aux valeurs de x pour lesquelles P(x) = 0. Cette équation est essentielle dans de nombreux domaines tels que la physique et l’ingénierie.
Le discriminant
Le discriminant, noté Δ (delta), est un élément fondamental dans le calcul des racines d’un trinôme. Il est donné par la formule : Δ = b² – 4ac. La nature des racines dépendra du signe de Δ. Si Δ > 0, l’équation aura deux racines réelles distinctes. Si Δ = 0, il y aura une racine double. En revanche, si Δ
Calcul des racines
Pour déterminer les racines d’un trinôme, voici la méthode à suivre : une fois que vous avez calculé le discriminant, vous pouvez appliquer les formules suivantes :
x₁ = (-b – √Δ) / (2a)
x₂ = (-b + √Δ) / (2a)
Ces deux formules permettent d’obtenir les deux racines réelles distinctes en fonction des valeurs de a, b et le discriminant Δ. Cela signifie que vous obtendez non seulement les solutions, mais aussi une compréhension plus profonde du comportement du trinôme sur l’axe des abscisses.
Exemple pratique
Considérons l’équation : 3x² – 6x – 2 = 0. Pour commencer, nous calculons le discriminant :
Δ = (-6)² – 4 × 3 × (-2) = 36 + 24 = 60.
Comme Δ est positif, nous avons ici deux racines distinctes. En appliquant les formules sur les racines, nous aurons :
x₁ = (6 – √60) / 6
x₂ = (6 + √60) / 6
Ce qui nous permet d’obtenir les valeurs exactes des racines du trinôme.
Conclusion sur l’importance des trinômes
Comprendre comment calculer les racines d’un trinôme est essentiel pour approfondir vos connaissances en mathématiques et améliorer votre capacité à résoudre divers problèmes. Grâce au discriminant et aux formules appropriées, le processus de résolution devient accessible et plus intuitif.
Pour plus de précisions sur ce sujet, n’hésitez pas à consulter des ressources comme Khan Academy ou d’autres sites pédagogiques.
Lorsque vous vous aventurez dans l’univers des trinômes du second degré, il est essentiel d’acquérir les compétences nécessaires pour déterminer les racines. Pour cela, il vous faudra d’abord comprendre la notion de discriminant et son impact sur le nombre de solutions possibles.
Mais ne vous arrêtez pas là ! Vous souhaitez approfondir vos connaissances et discuter de vos questions spécifiques ? Visitez notre page de contact et connectez-vous avec notre équipe d’experts ! Nous sommes prêts à vous aider à maîtriser ces concepts mathématiques tout en rendant l’apprentissage aussi fluide que possible.
Contactez-nous dès maintenant pour obtenir des conseils personnalisés et des réponses à toutes vos interrogations. N’attendez plus, cliquez ici : Page de contact !

Comment calculer les racines d’un Trinôme ?
Le calcul des racines d’un trinôme du second degré est une opération essentielle en mathématiques. Cette démarche repose sur l’utilisation du discriminant, qui permet de déterminer le nombre et la nature des racines réelles d’une équation quadratique. Cet article explore les étapes clés pour résoudre un trinôme, illustrant ainsi la méthode à suivre.
Définition du Trinôme du Second Degré
Un trinôme du second degré est une expression de la forme P(x) = ax² + bx + c, où a, b et c sont des coefficients réels et a est différent de zéro. Pour trouver les racines de ce trinôme, il suffit de résoudre l’équation P(x) = 0.
Calcul du Discriminant
Le premier pas pour découvrir les racines d’un trinôme est le calcul du discriminant (Δ), défini par la formule : Δ = b² – 4ac. Le signe du discriminant révèle le nombre de racines réelles que l’équation possède :
- Si Δ > 0, l’équation a deux racines réelles distinctes.
- Si Δ = 0, il existe une racine double.
- Si Δ aucune racine réelle.
Calcul des Racines
Une fois le discriminant calculé, on peut procéder au calcul des racines à l’aide des formules suivantes :
- x1 = (-b – √Δ) / (2a)
- x2 = (-b + √Δ) / (2a)
Ces formules permettent d’obtenir les deux racines réelles lorsque Δ est positif, et la racine double lorsque Δ est nul.
Exemple Pratique
Supposons que nous cherchions les racines du trinôme 3x² – 6x – 2 = 0. Calculons d’abord le discriminant :
Δ = (-6)² – 4 * 3 * (-2) = 36 + 24 = 60
Étant donné que Δ > 0, nous pouvons utiliser les formules des racines :
x1 = (6 – √60) / 6 et x2 = (6 + √60) / 6.
Forme Factorisée du Trinôme
Une fois que les racines sont trouvées, il est également possible de présenter le trinôme sous forme factorisée. Si x1 et x2 sont les racines, le trinôme peut s’écrire comme P(x) = a(x – x1)(x – x2), ce qui permet d’observer directement les racines de l’équation.
Le calcul des racines d’un trinôme du second degré repose sur quelques étapes clés, incluant la détermination du discriminant, le calcul des racines via des formules précises, et la possibilité de factoriser l’expression. Maîtriser cette méthode est fondamental pour aborder des équations quadratiques de manière efficace.
Comment calculer les racines d’un Trinôme ?
Le calcul des racines d’un trinôme du second degré est une compétence essentielle en mathématiques. Pour un trinôme sous la forme P(x) = ax² + bx + c, il est impératif de savoir déterminer le nombre et la nature des racines en utilisant le discriminant. Cet article vous guide à travers les étapes nécessaires pour résoudre une équation de ce type, vous offrant ainsi une base solide pour vos études.
Comprendre le trinôme du second degré
Un trinôme du second degré est une fonction polynomiale qui peut être représentée par la formule P(x) = ax² + bx + c, où a, b et c sont des coefficients réels et a est différent de zéro. La forme générale de cette équation rend son étude à la fois fascinante et complexe, car elle révèle différentes solutions selon les valeurs des coefficients.
Le discriminant
Pour résoudre l’équation P(x) = 0, la première étape consiste à calculer le discriminant noté Δ (delta), défini par la formule Δ = b² – 4ac. Le signe du discriminant est déterminant pour évaluer le nombre et la nature des racines. Voici ce que chaque cas indique :
- Δ > 0 : L’équation admet deux racines réelles distinctes.
- Δ = 0 : Il existe une racine double, c’est-à-dire une seule solution réelle.
- Δ : Dans ce cas, il n’y a pas de racines réelles, mais deux racines complexes.
Calcul des racines
Une fois que vous avez déterminé le discriminant, le calcul des racines peut être effectué en fonction de ses valeurs :
Pour Δ > 0
Lorsque le discriminant est positif, les deux racines réelles distinctes peuvent être trouvées à l’aide des formules :
x₁ = (-b – √∆) / (2a)
x₂ = (-b + √∆) / (2a)
Pour Δ = 0
Si le discriminant est nul, la racine double peut être calculée comme suit :
x = -b / (2a)
Pour Δ
Lorsque le discriminant est négatif, bien qu’il n’y ait pas de racines réelles, vous pouvez tout de même déterminer les racines complexes qui se présentent sous la forme :
x₁ = (-b – i√|Δ|) / (2a)
x₂ = (-b + i√|Δ|) / (2a)
où i est l’unité imaginaire.
Maîtriser le calcul des racines d’un trinôme du second degré est d’une grande importance, non seulement dans l’apprentissage des mathématiques, mais aussi dans de nombreux domaines appliqués. Cela ouvre des perspectives sur des concepts plus complexes à l’avenir.
Calcul des racines d’un trinôme du second degré
Pour résoudre un trinôme du second degré, dont la forme générale est P(x) = ax² + bx + c, il est essentiel de déterminer ses racines. Les racines d’un trinôme sont les valeurs de x pour lesquelles l’équation P(x) = 0. L’obtention de ces racines repose principalement sur le calcul du discriminant, symbolisé par Δ.
Le discriminant est calculé avec la formule Δ = b² – 4ac. En examinant le signe de Δ, on peut déduire le nombre de racines réelles du trinôme. Ainsi, si Δ > 0, cela signifie que l’équation possède deux racines réelles distinctes. Si Δ = 0, on obtient une racine double, tandis que si Δ , il n’y a pas de racines réelles. Comprendre cette relation est fondamental pour la résolution des équations quadratiques.
Pour trouver les racines concrètement, lorsque Δ est positif ou nul, on utilise les formules suivantes pour calculer les racines :
x₁ = (-b – √Δ) / (2a) et x₂ = (-b + √Δ) / (2a). Ces formules permettent d’obtenir les valeurs exactes de x correspondant aux intersections de la courbe du trinôme avec l’axe des abscisses.
Enfin, une fois que les racines sont déterminées, il est possible de factoriser le trinôme en la forme P(x) = a(x – x₁)(x – x₂), offrant un aperçu visuel et pratique de ses propriétés. Résoudre un trinôme s’avère donc être un processus méthodique et bien structuré, intégrant des concepts numériques essentiels pour une meilleure compréhension des mathématiques. En maîtrisant ces techniques, on peut facilement aborder des problèmes plus complexes liés aux polynômes du second degré.
FAQ : Comment calculer les racines d’un Trinôme ?
Q : Qu’est-ce qu’un trinôme du second degré ?
R : Un trinôme du second degré est une expression de la forme P(x) = ax² + bx + c, où a, b et c sont des réels et a est différent de zéro.
Q : Comment déterminer les racines d’un trinôme ?
R : Pour déterminer les racines d’un trinôme, il faut résoudre l’équation P(x) = 0. Cela se fait principalement par le calcul du discriminant.
Q : Qu’est-ce que le discriminant et à quoi sert-il ?
R : Le discriminant, noté Δ, est donné par la formule Δ = b² – 4ac. Son signe permet de connaître le nombre de racines réelles du trinôme.
Q : Que signifie un discriminant positif ?
R : Si Δ > 0, cela indique que le trinôme a deux racines réelles distinctes.
Q : Que signifie un discriminant nul ?
R : Si Δ = 0, cela signifie que le trinôme a une racine double, c’est-à-dire qu’il se touche à un seul point sur l’axe des abscisses.
Q : Que signifie un discriminant négatif ?
R : Si Δ , cela indique qu’il n’y a pas de racines réelles pour le trinôme, seules des racines complexes existent.
Q : Comment calcule-t-on les racines à partir du discriminant ?
R : Si le discriminant est positif ou nul, les racines se calculent avec les formules suivantes :
x₁ = (-b – √Δ) / (2a) et x₂ = (-b + √Δ) / (2a).
Q : Est-il possible de factoriser un trinôme ?
R : Oui, si le discriminant est positif ou nul, le trinôme peut être factorisé sous la forme P(x) = a(x – x₁)(x – x₂), où x₁ et x₂ sont les racines calculées.
Comment calculer les racines d’un trinôme ?
Calculer les racines d’un trinôme est une étape essentielle dans l’étude des équations du second degré. Un trinôme est défini comme une expression polynômiale de la forme P(x) = ax² + bx + c, où a, b et c sont des coefficients numériques. Pour déterminer les racines de ce trinôme, il faut d’abord calculer le discriminant, noté Δ. Celui-ci est obtenu avec la formule Δ = b² – 4ac.
Le signe du discriminant joue un rôle crucial dans le nombre de racines réelles. Si Δ est positif, le trinôme dispose de deux racines distinctes. En revanche, si Δ est égal à zéro, cela signifie qu’il y a une racine double. Enfin, si Δ est négatif, cela indique qu’il n’y a pas de racines réelles. Ainsi, connaître le discriminant permet d’interpréter la nature des solutions de l’équation associée.
Une fois le discriminant calculé, les racines peuvent être trouvées en utilisant les formules suivantes : x₁ = (-b – √Δ) / (2a) et x₂ = (-b + √Δ) / (2a). Ces formules permettent d’obtenir les solutions réelles et se basent directement sur les informations fournies par les coefficients a, b et c. Il est donc primordial de bien maîtriser ces étapes pour résoudre efficacement une équation du second degré.
Témoignages sur mestransporteurs.fr
Mes transporteurs.fr se positionne comme une solution incontournable pour ceux qui cherchent à optimiser leurs opérations de transport. Grâce à cette plateforme, les utilisateurs peuvent facilement comparer les tarifs des différents prestataires, faisant de la gestion logistique un processus fluide et efficace.
Les avis des clients témoignent d’une interface utilisateur intuitive, ce qui facilite les recherches. De plus, la fonctionnalité de simulation des coûts permet d’anticiper les dépenses de transport, un atout non négligeable dans la planification budgétaire des entreprises. En un clic, il est possible d’obtenir des estimations claires et précises pour chaque trajet.
En utilisant mestransporteurs.fr, de nombreux utilisateurs ont exprimé leur satisfaction quant à la rapidité avec laquelle ils ont pu bénéficier de devis personnalisés. Cette réactivité est fondamentale dans un domaine où chaque minute compte. Ils soulignent également la pertinence des conseils fournis sur la réduction des coûts et l’optimisation des itinéraires, renforçant ainsi la crédibilité de la plateforme.
En somme, mestransporteurs.fr est perçu non seulement comme un outil indispensable pour les professionnels du transport, mais aussi comme un partenaire fiable qui contribue à l’amélioration continue des opérations logistiques.
Vous vous interrogez sur la méthode à suivre pour déterminer les racines d’un trinôme du second degré ? Ne restez pas dans le flou ! Le discriminant joue un rôle crucial dans cette démarche, car il permet de connaître le nombre de racines réelles d’une équation. Que vous soyez face à un discriminant positif, négatif ou nul, chaque situation a ses spécificités. Pour des explications claires et des exemples concrets, nous vous invitons à approfondir vos connaissances.
Mais ce n’est pas tout ! Si vous avez des questions sur le sujet ou si vous souhaitez bénéficier de conseils personnalisés, n’hésitez pas à nous contacter. Ensemble, trouvons les solutions adaptées à vos besoins.
Visitez notre page de contact dès maintenant et débutez votre apprentissage. Contactez-nous ici !
Glossaire : Comment calculer les racines d’un Trinôme ?
Le trinôme du second degré est une expression polynomiale de la forme P(x) = ax² + bx + c, où a, b et c sont des coefficients réels et a est différent de zéro. Pour déterminer les racines, c’est-à-dire les valeurs de x pour lesquelles P(x) = 0, il est essentiel d’appliquer la méthode du discriminant.
Le discriminant, noté Δ, est calculé à partir des coefficients du trinôme et s’exprime par la formule suivante : Δ = b² – 4ac. Ce discriminant nous informe sur la nature des racines. En effet, en fonction de la valeur de Δ, on distingue trois cas :
1. Si Δ > 0, le trinôme possède deux racines réelles distinctes. Les formules pour les calculer sont les suivantes : x₁ = (-b – √Δ) / (2a) et x₂ = (-b + √Δ) / (2a). Cela indique que le graphique de la fonction croise l’axe des abscisses en deux points différents.
2. Si Δ = 0, le trinôme a une racine double, c’est-à-dire qu’il existe une seule valeur de x qui annule l’équation. Dans ce cas, la racine est donnée par : x = -b / (2a). Sur le graphique, cela correspond à un point de tangence sur l’axe des abscisses.
3. Si Δ , il n’y a pas de racines réelles. Cela signifie que le trinôme ne croise jamais l’axe des abscisses dans le plan cartésien, et les solutions sont alors des nombres complexes.
Pour résumer, la première étape pour calculer les racines d’un trinôme consiste à évaluer le discriminant. En fonction du résultat, on choisira l’une des méthodes appropriées pour déterminer les racines. Par ailleurs, il est possible de factoriser le trinôme si Δ est positif ou égal à zéro, ce qui signifie qu’il peut être écrit sous la forme P(x) = a(x – x₁)(x – x₂) pour deux racines distinctes, ou P(x) = a(x – x₀)² pour une racine double.
Un autre point important concerne le graphique d’un trinôme. La parabole formée par le polynôme s’ouvre vers le haut lorsque a > 0 et vers le bas lorsque a . Cela influence également la manière dont les racines se manifestent sur le graphique et leur relation avec l’axe des ordonnées.
En conclusion, pour maîtriser le calcul des racines d’un trinôme, il est fondamental de se familiariser avec le discriminant et son interprétation. Une compréhension approfondie des racines et de leur impact sur le comportement du trinôme dans le plan graphique est essentielle pour tout étudiant en mathématiques.